Foundation of Robotics from Math to Control - Course (1) : Kinematics
- Description
- Curriculum
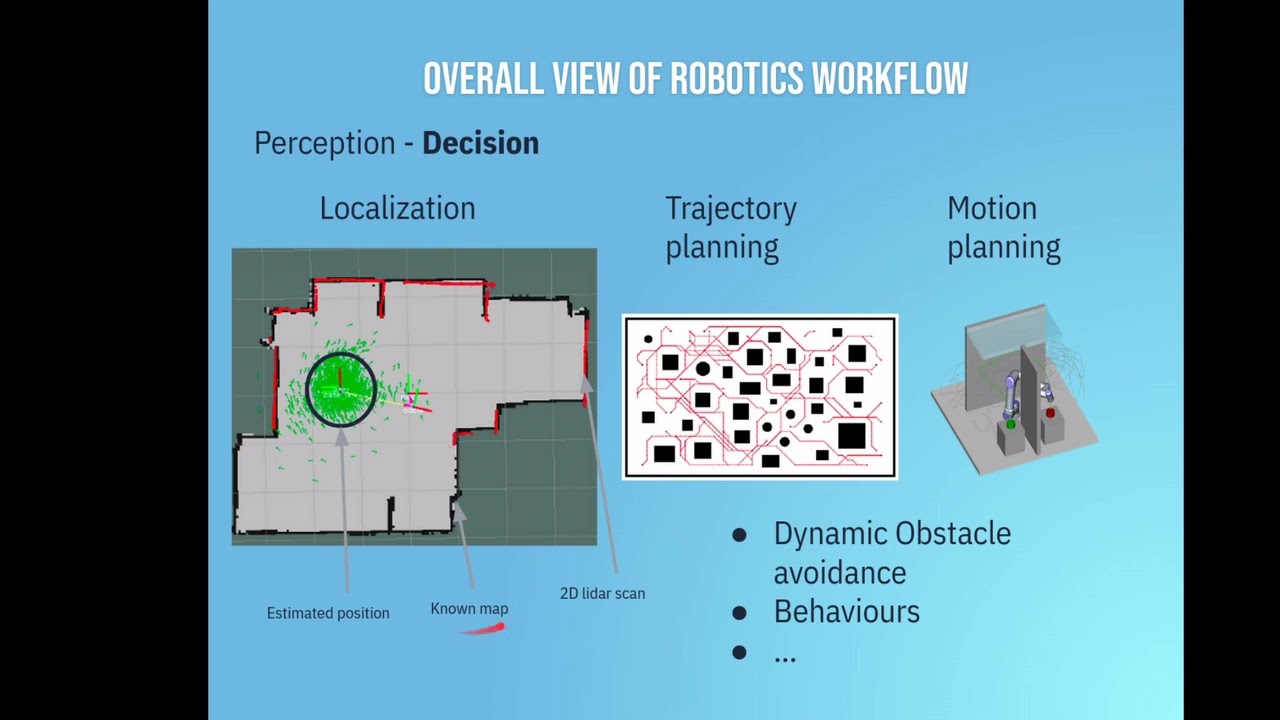
🎓 Course Title: Foundations of Robotics: From Math to Control
🔍 Prerequisites
To make the most of this course, students should have:
-
A basic understanding of derivatives
-
Foundational knowledge in linear algebra
-
General physics concepts such as angular and linear velocity, acceleration, and momentum
-
While the majority of the course is delivered in Arabic, a basic understanding of English is recommended to follow technical terminology and project content
📘 Course 1 – Kinematics
This course introduces the essential mathematical foundations required for understanding and working with robotic systems. Topics include:
-
Vectors, matrices, and spatial transformations in both 2D and 3D
-
Representation and manipulation of rigid body motion using Python examples
-
Derivation of forward kinematics for robotic manipulators using two key methods:
-
Denavit–Hartenberg (D-H) Convention
-
Product of Exponentials (PoE)
-
By the end of this course, students will be able to mathematically model robotic arms and simulate their motion, forming a critical base for more advanced topics in dynamics and control.
-
1
Chapter 0: Definitions and motivation -
2
Chapter 0: Definitions and motivationThis introductory chapter sets the stage for the course by defining robotics and outlining its interdisciplinary nature. It also provides a clear overview of what to expect in the upcoming modules.
-
3
Chapter 1: Mathematical Foundations for Robotics
This chapter lays the essential mathematical groundwork for robotics. Students will review key concepts in linear algebra and apply them using Python, building the skills necessary for deeper exploration in kinematics and control.
-
4
Chapter 2: Spatial transformation and rigid body motion
This chapter introduces the fundamental mathematical tools for describing motion in two and three dimensions, focusing on spatial transformations essential in robotics and control systems. Through theory, visualization, and coding examples, students will gain a strong foundation in rigid body kinematics.
-
5
Chapter 3: Forward Kinematics
This chapter delves into forward kinematics, a core concept in robotics that maps joint parameters to end-effector positions. Students will explore both classical and modern approaches, compare their advantages, and apply them through practical programming examples.
